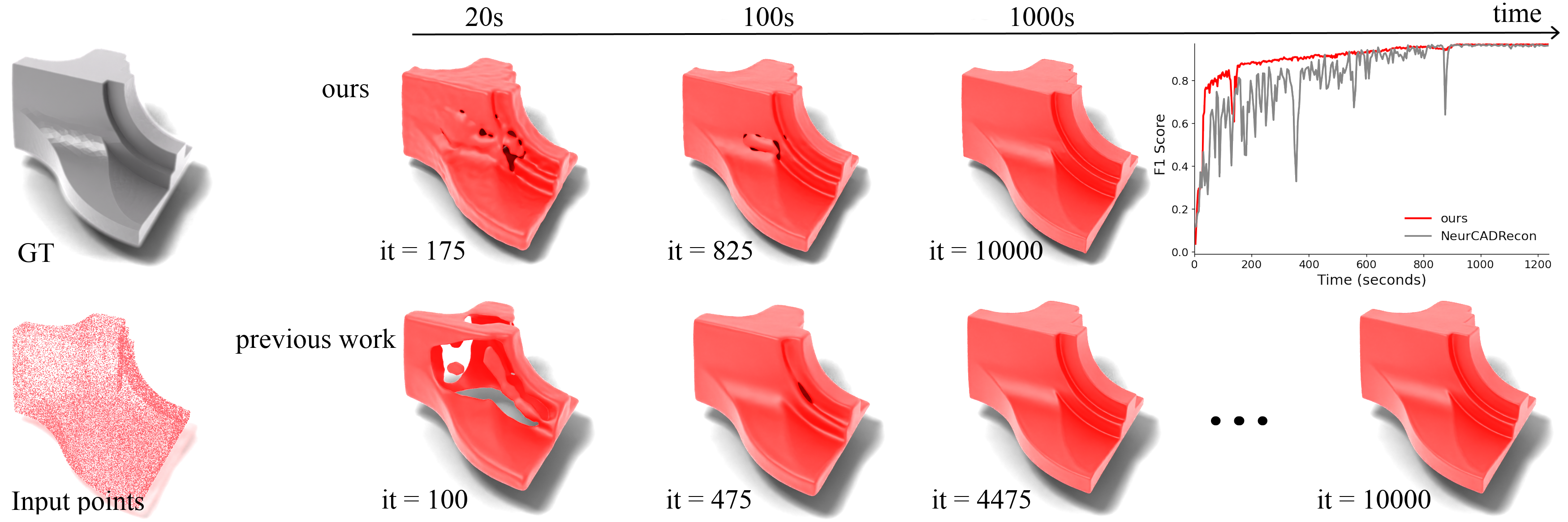
A Finite Difference Approximation of Second Order Regularization of Neural-SDFs
This work proposes a lightweight alternative to second-order automatic differentiation for Neural SDFs. Using finite-difference stencils with O(h2) truncation error, it approximates Gaussian curvature penalties efficiently, maintaining robustness on sparse data while reducing computational overhead by a factor of two.
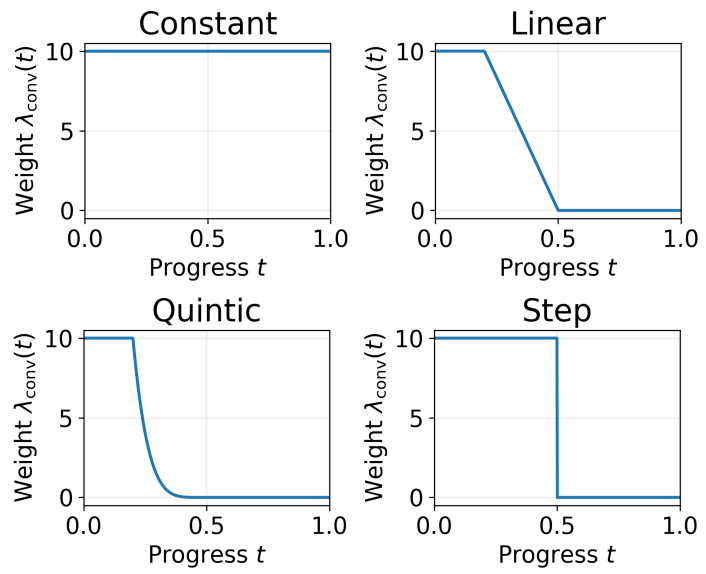
Scheduling the Off-Diagonal Weingarten Loss of Neural SDFs for CAD Models
A dynamic scheduling extension for the FlatCAD curvature loss. By decaying the regularization weight over the course of training, this method balances optimization stability with fine-scale detail recovery, achieving a 35% improvement in reconstruction fidelity compared to the fixed-weight baseline.
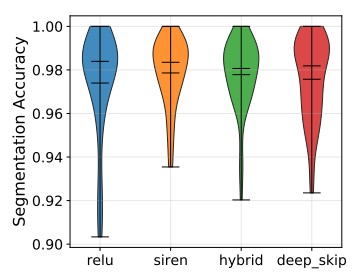
Joint Neural SDF Reconstruction and Semantic Segmentation for CAD Models
This method augments a neural SDF backbone with a lightweight segmentation head, enabling simultaneous shape reconstruction and part labeling. Unlike approaches tied to fixed taxonomies, the pipeline handles arbitrary part counts using PartField supervision. It delivers strong segmentation accuracy and label coherence, even on intricate geometries where reconstruction quality might degrade.